Model Method - Questions and Answers

Question posted by Yvonne from Sri Lanka:

Grade/Level: 4th

Question solved by Model Method: 900 people attended a party. 1/4 of the males and 1/7 of the females were children. the number of male and female adults were the same. how many women were there at the party?

Answer:


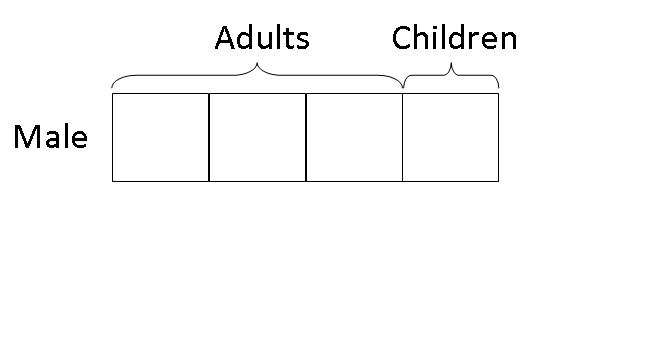
Step 1: This question involves the Equal Concept. Since 1/4 of the males were children, then 3/4 of the males must be adults. We draw 3 boxes to represent the total number of male adults and 1 box to represent the total number of male children.

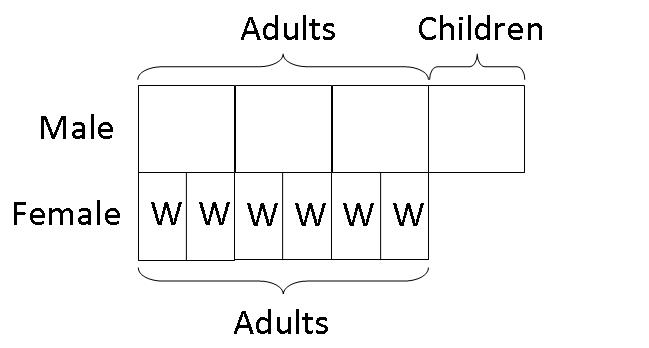
Step 2: Since 1/7 of the females were children, then 6/7 of the females must be adults. We were also given that the number of male and female adults were the same. Thus, 3/4 of the males(men) must be equal to 6/7 of females(women). So we draw 6 units of women to be equivalent to 3 big boxes representing all the men.

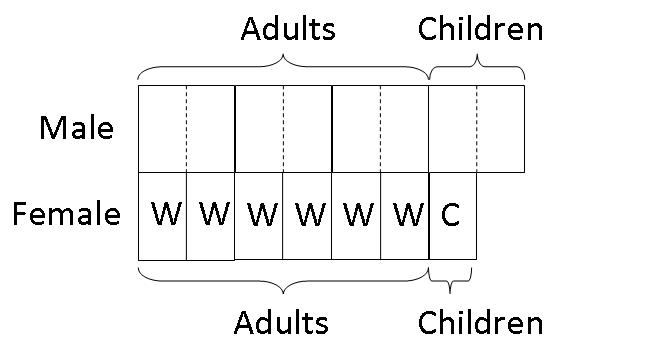
Step 3: Next, since each big box representing the males is equivalent to 2 small boxes representing the females, we divide each big box into 2 small boxes. We also add in 1 small box to represent 1/7 of the females (which are the female children).

Step 4: We then label 6 small boxes as "M" (men) and 2 small boxes as "C" (male children or boys). We also add in a bracket to the right to denote the total number of people (900) who attended the party.

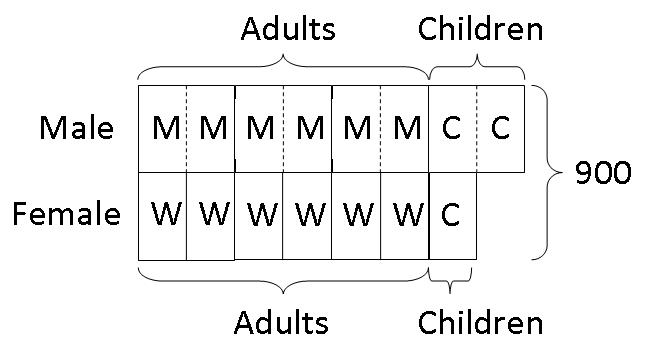
From the model,

15 units ---------- 900 people

1 unit ---------- 900 people / 15 = 60 people

6 units ---------- 6 x 60 people = 360 people

Therefore, there were 360 women at the party.

Go To Top - Model Method - Questions and Answers


If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!