The Constant Difference Concept
Comparison Concept . This concept is applicable when the problems deal with an equal quantity being transferred in or transferred out of the two variables concerned. This leaves the two variables with an equal increase or decrease in value. The unique feature in this concept lies in the fact that after the transfer in or transfer out of quantities, the difference between the two variables remains unchanged, hence the name "Constant Difference" Concept.
To illustrate this concept, take a look at the following problems.
(A) Equal Amount Transferred into 2 Variables
Question: Ken had 14 pens and Ben had 2 pens. When they received an equal number of pens from their teacher, the ratio of Ken's pens to Ben's pens became 3:1. How many pens did each of them receive from their teacher?
Answer: For this question, we will work backwards. It is always easier to start drawing models where a multiples-relationship exist, i.e., a variable is a multiple of another variable. In this example, Ken is 3 times of Ben after the transfer in.
Step 1: Since the ratio of Ken's pens to Ben's pens after the transfer in is 3:1, we draw 3 boxes to represent the number of units that Ken had and 1 box to represent the number of units that Ben had.
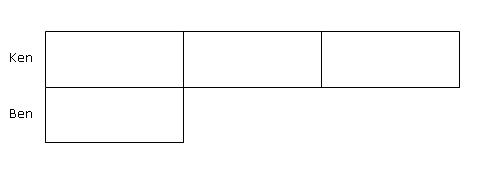
Step 2: Since an equal amount was transferred in, we mark out an equal amount from both Ken's and Ben's model bars to show this amount.
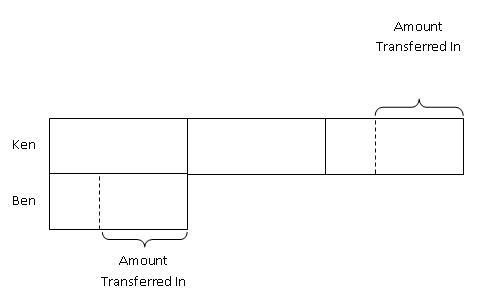
Step 3: Next, we label the models with the number of pens they each had at first.
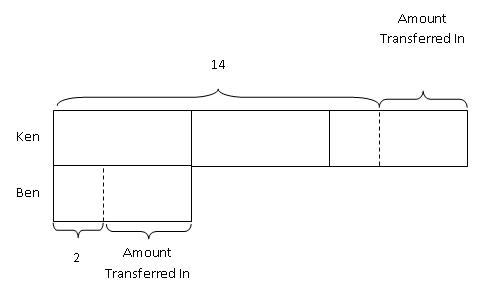
Step 4: After all information have been put into the model, we can then mark out all the known parts and try to make all the unknown parts equal.
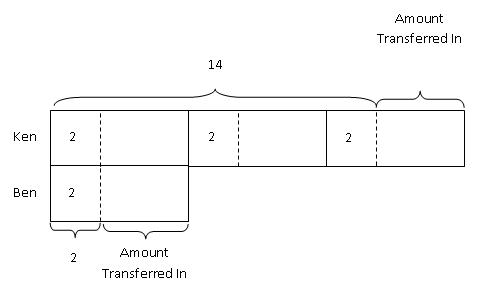
Step 5: From Ken's bar, we can see that,
2 units + 2 pens + 2 pens + 2 pens ----------> 14 pens
2 units + 6 pens ----------> 14 pens
2 units ----------> 14 pens - 6 pens = 8 pens
1 unit ----------> 8 pens / 2 units = 4 pens
Thus, they reach receive 4 pens from their teacher.
(B) Equal Amount Transferred out of 2 Variables
Question: Chloe had 18 stickers and Jane had 6 stickers. When they both gave away an equal number of stickers, Chloe had 4 times as many stickers as Jane. How many stickers did they each gave away?
Answer: For this question, we will again work backwards. It is always easier to start drawing models where a multiples-relationship exist, i.e., a variable is a multiple of another variable. In this example, Chloe is 4 times of Jane after the transfer out.
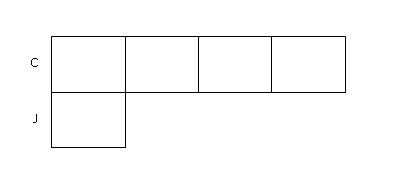
Step 1: Since the ratio of Chloe's pens to Jane's pens after the transfer out is 4:1, we draw 4 boxes to represent the number of units that Chloe had and 1 box to represent the number of units that Jane had.
Step 2: Since an equal amount was transferred out, we add an equal amount back to represent the part that each of them gave away.
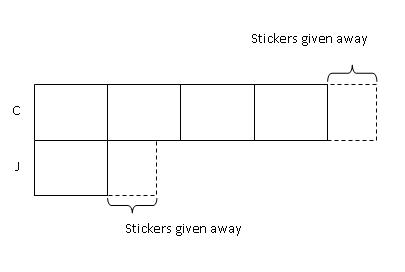
Step 3: Next, we label the models with the number of stickers they each had at first.
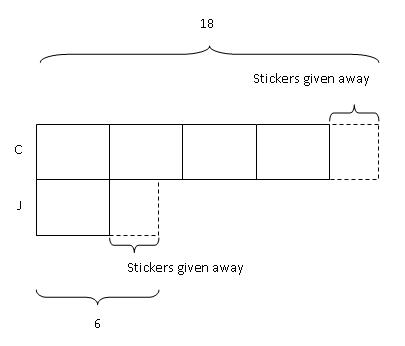
Step 4: Rearrange the units in Chloe's bar.
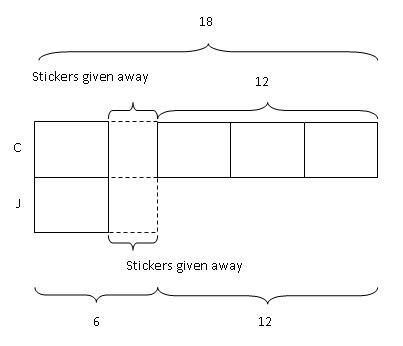
From the model, we can see that after we shift the last unit of Chloe's bar forward, the remaining 3 unknown but equal units add up to 12.
3 units ----------> 12 stickers
1 unit -----------> 12 stickers / 3 = 4 stickers
Step 5: Putting the value of 4 stickers per unit back into the model, we get:
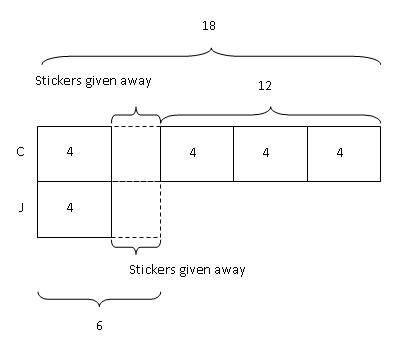
Looking at Jane's model,
6 stickers - 4 stickers = 2 stickers
Therefore, they each gave away 2 stickers.
(C) Age Difference
Question: Matthew is 29 years old and his son is 5 yrs old now. In how many years will Matthew be thrice as old as his son?
Answer: In such questions, do bear in mind that the age difference between any 2 persons will always remain a constant.
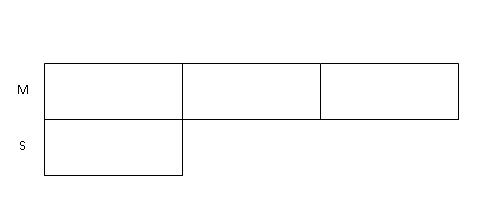
Step 1: It is easier to draw the "After" model first and work backwards to the "Before" model. First, we draw 3 boxes to represent Matthew's age and 1 box to represent the son's age after their age increases.
Step 2: Since an equal amount was added to their ages, we mark out an equal box on both their model bars to represent the number of years they have grown from their present age.
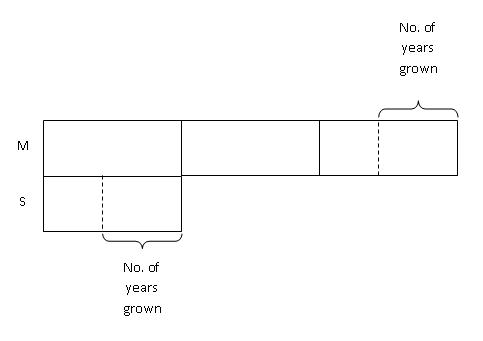
Step 3: Next, we label the models with their present age.

Step 4: We then divide the model to reflect the known and unknown units.
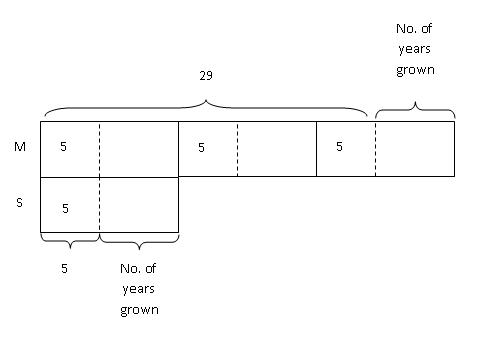
From the model,
2 units + 5 years + 5 years + 5 years ----------> 29 years
2 units + 15 years ----------> 29 years
2 units ----------> 29 years - 15 years
2 units ----------> 14 years
1 unit ----------> 14 years / 2 = 7 years
Therefore, Matthew will be thrice as old as his son in 7 years' time.
Go To Top - Constant Difference Concept
If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!




