The Constant Total Concept
Comparison Concept and the Change Concept . This concept is applicable when the problems deal with two variables transferring quantities to each other leaving the total unchanged, hence the name "Constant Total Concept". The unique feature in this concept lies in the fact that in the problem, it can be a one-way or two-way transfer. In a one-way transfer, one variable transfer some quantities to the other variable leaving the total unchanged. In a two-way transfer, the two variables each gives some quantities to the other party, leaving both variables' total unchanged.
To illustrate the Constant Total Concept, take a look at the following problems.
(A) One-Way Transfer
Class A had 1/3 the number of pupils in Class B. After 14 pupils were transferred from Class B to Class A, Class A had 4/5 the number of pupils in Class B. How many pupils were there in Class A at first?
Answer:
Step 1: Draw the "Before" model for both classes, 1 box to represent Class A and 3 boxes to represent Class B, since Class A is 1/3 of Class B.
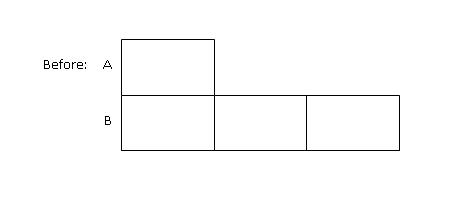
Step 2 : Draw the "After" model for both classes, 4 boxes to represent Class A and 5 boxes to represent Class B, since Class A is 4/5 of Class B.
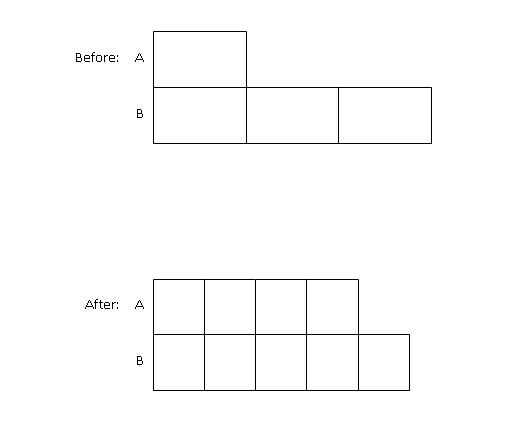
From the model, we know that before the transfer, the total number of units is 4 units and after the transfer, the total number of units is 9 units. As this is purely an internal transfer of quantities not involving any external parties, the 4 units in the "Before" model must be equivalent to the 9 units in the "After" model.
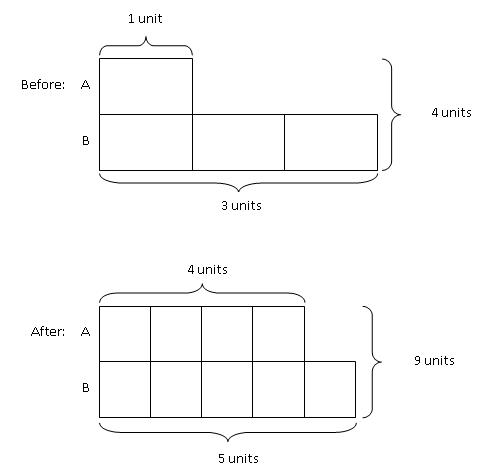
We need to find a common multiple for the two totals to make the comparison meaningful. A common multiple of 4 and 9 would be 36.
Step 4: Thus, we divide both the "Before" and "After" models into 36 units each.
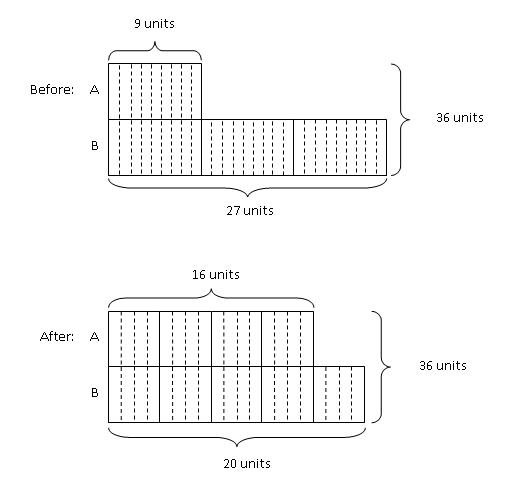
From the model, we can see that 7 units was transferred from Class B to Class A. Since 14 pupils were transferred from Class B to Class A,
7 units -------> 14 pupils
1 unit --------> 14 pupils / 7 units = 2 pupils
9 units -------> 9 units X 2 pupils = 18 pupils
Therefore, Class A had 18 pupils at first.
(B) Two-Way Transfer
Roger had twice as many marbles as Mark at first. Mark gave 1/2 of his marbles to Roger and Roger gave 3/5 of his marbles back to Mark. In the end, Mark had 8 more marbles than Roger. How many marbles did each of them have at first?
Answer:
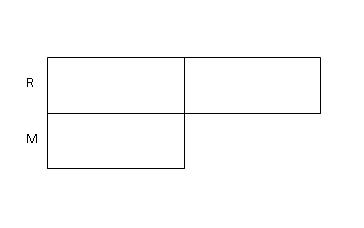
Step 1: Draw 2 boxes to represent the number of marbles that Roger had and 1 box to represent the number of marbles that Mark had.
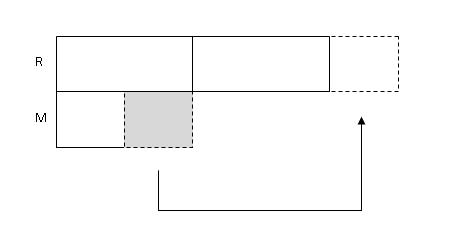
Step 2: Since Mark gave 1/2 of his marbles to Roger, we divide his bar into 2 boxes and transfer 1 box to Roger.
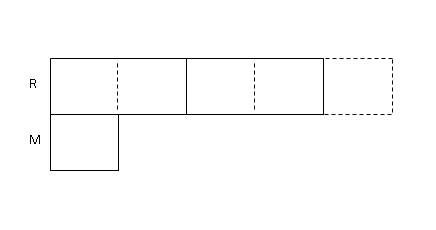
Step 3: For ease of comparison, we divide all the other boxes that Roger had into 2 smaller boxes as well. Now we have all the unknown boxes as equal units.
Step 4: Since Roger then gave 3/5 of his marbles back to Mark, we transfer 3 units out of his 5 units back to Mark.
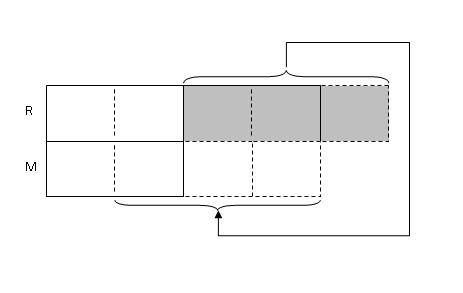
Step 5: In the end, Mark had 8 more marbles than Roger (given in the question).
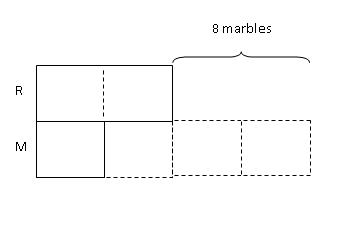
From the model,
2 units -------> 8 marbles
1 unit --------> 8 marbles / 2 units = 4 marbles
4 units -------> 4 units X 4 marbles = 16 marbles
Therefore, Roger had 16 marbles and Mark had 8 marbles at first.
Go To Top - Constant Total Concept
If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!




