The Remainder Concept
Part-Whole Concept . Very often, questions which require the use of this Concept have the word "remainder" embedded in them. In this concept, we first draw a model to represent the whole and mark out the parts that were used or taken away from the whole. Then the "remainder part" of the model is subdivided according to the requirements given in the question. Eventually, all the known parts should be properly labelled with values and all the unknown parts should be divided equally so that we can work out their values.
To illustrate this concept, consider the following question,
Brandon gave 1/5 of his monthly salary to his mother. He gave 3/4 of the remainder to his wife and saved the rest each month. He managed to save $400 every month. How much did he earn a month?
Step 1: Draw a long bar to represent the total of his salary.
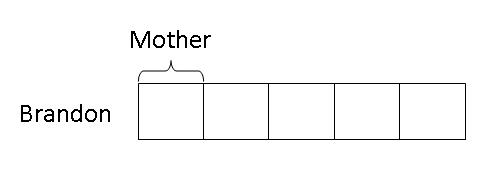
Step 2: Divide the model into 5 equal parts and label 1 part as given to his mother.
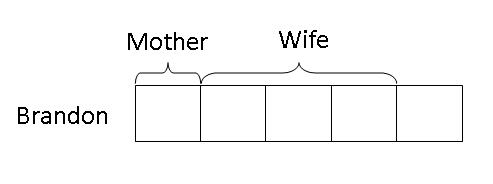
Step 3: Notice that there are 4 units left after giving 1/5 of his salary to his mother. Since he gave 3/4 of his salary to his wife, we label 3 of the remaining 4 units as given to his wife(3/4 is 3 out of 4 equal units).
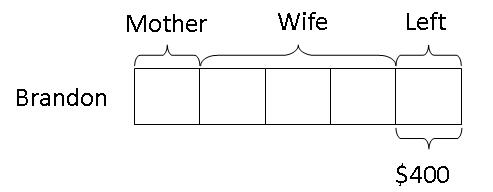
Step 4: Since he had $400 left after that and there is only 1 unit of the model left, the last unit must be equal to $400.
Hence,
1 unit ----------> $400
5 units ----------> 5 X $400 = $2000
Therefore, Brandon earns $2000 a month.
If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!




