The Change Concept
Part-Whole Concept and the Comparison Concept . You will, however, noticed that the Change Concept is seemingly familiar when compared with the Part-Whole Concept and the Comparison Concept. The Singapore Math Primary Curriculum adopts a concrete-pictorial-abstract progressive approach to help pupils tackle seemingly difficult and challenging word problems. Mathematics Teachers in Singapore usually make use of concrete objects to allow students to make sense of the relationship between the new value of a quantity and its original value after an increase or decrease takes place. Once the pupils can visualize the change caused by the increase or decrease in quantity, they will then move on to put these relationships in rectangular bars as pictorial representations of the math models concerned.
To illustrate the change concept involving an increase, take a look at the following problem:
Peter has 3 marbles. Caleb gives Peter 1 more marble. How many marbles does Peter have now?
We can first give the child concrete objects, like 3 marbles and another 1 marble, and let the child display the 3 marbles first and increase the total of the group by putting in 1 extra marble into the group to find the new value after the increase of 1 marble.
When they are comfortable with increasing the original value to the new value with the concrete objects, we can then proceed to teach them to draw pictures of the concrete objects within boxes to illustrate the equation 3 + 1 = 4
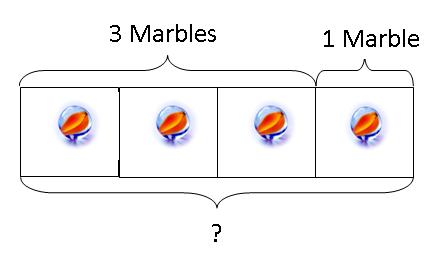
After that, we can teach the kids to go on to draw the boxes without the objects.
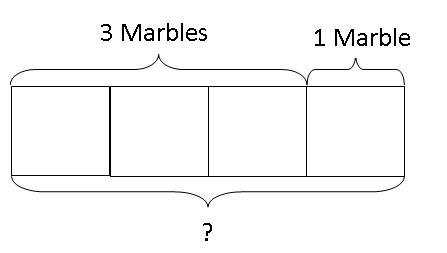
Eventually, the equation can be visualised as an original value being increase by a certain value to obtain the new value. To find the new value after the increase for the above problem, they just need to add the "increase" to the original value.
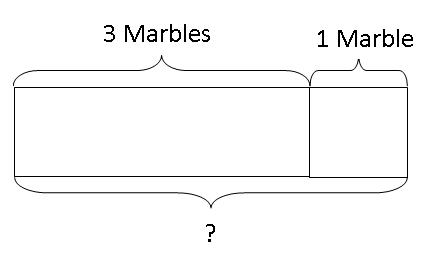
So, 3 + 1 = 4
Therefore, Peter has 4 marbles now.
Hence, we can see that the relationship among the original value, the increase and the new value can be summarised as follows:
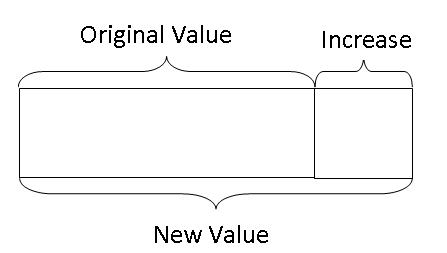
To find the new value given the original value and the increase, just add the increase to the original value:
Original Value + Increase = New Value
To find the original value given the new value and the increase, just subtract the increase from the new value:
New Value - Increase = Original Value
To find the increase given the new value and the original value, just subtract the original value from the new value:
New Value - Original Value = Increase
To illustrate the change concept involving a decrease, take a look at the following problem:
Peter has 3 marbles. Peter gives away 1 marble to Caleb. How many marbles does Peter have now?
We can first give the child concrete objects, like 3 marbles, and let the child display the 3 marbles first and decrease the total of the group by taking away 1 marble from the group to find the new value after the decrease of 1 marble.
When they are comfortable with decreasing the original value to the new value with the concrete objects, we can then proceed to teach them to draw pictures of the concrete objects within boxes to illustrate the equation 3 - 1 = 2
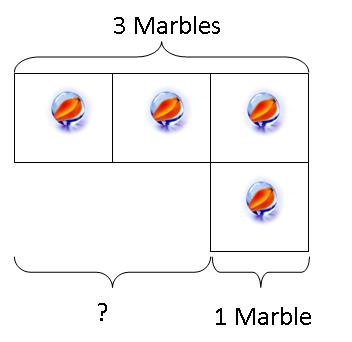
After that, we can teach the kids to go on to draw the boxes without the objects.
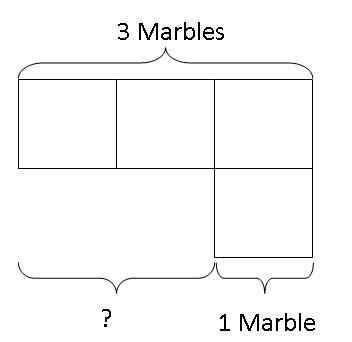
Eventually, the equation can be visualised as an original value being decrease by a certain value to obtain the new value. To find the new value after the decrease for the above problem, they just need to subtract the "decrease" from the original value.
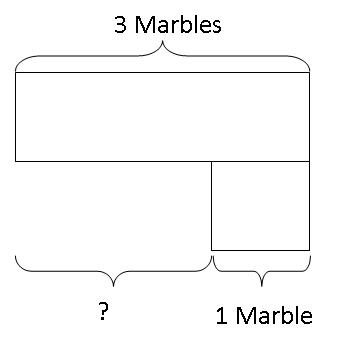
So, 3 - 1 = 2
Therefore, Peter has 2 marbles now.
Hence, we can see that the relationship among the original value, the decrease and the new value can be summarised as follows:
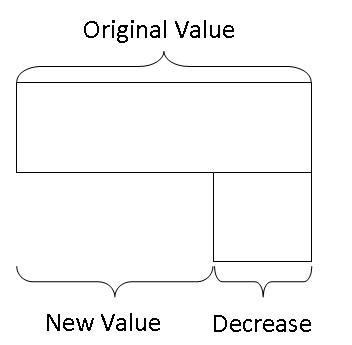
To find the new value given the original value and the decrease, just subtract the decrease from the original value:
Original Value - Decrease = New Value
To find the original value given the new value and the decrease, just add the decrease to the new value:
New Value + Decrease = Original Value
To find the decrease given the new value and the original value, just subtract the new value from the original value:
Original Value - New Value = Decrease
If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!




