Model Method - Questions and Answers
Question posted by Anonymous from Country Unknown:
Grade/Level: 5th Grade
Question: A is 40% of his brother's age. In 21 years time, A is 75% of his brother's age. What is A's age now?
Answer:
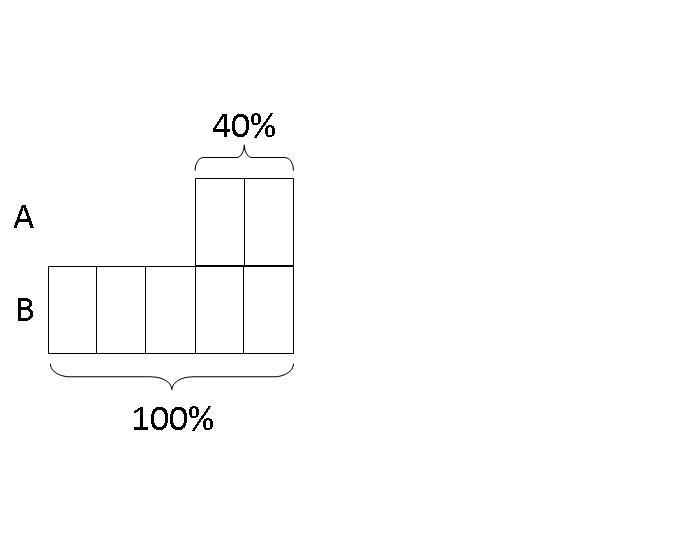
Step 1: This question involves the Constant Difference Concept. For Percentage questions, more often than not, it is easier to convert the percentages to fractions to facilitate drawing of models. Since A is 40% of his brother's age, we draw 2 boxes to represent A's 40% and 5 boxes to represent his brother's 100%. Please take note that we draw both A and his brother's model justified to the right because we intend to add an equal bar to the right of both of their models to show they have both grown an equal number of year, i.e., 21 years. This way of drawing the model will greatly facilitate the comparison of the 2 models subsequently.
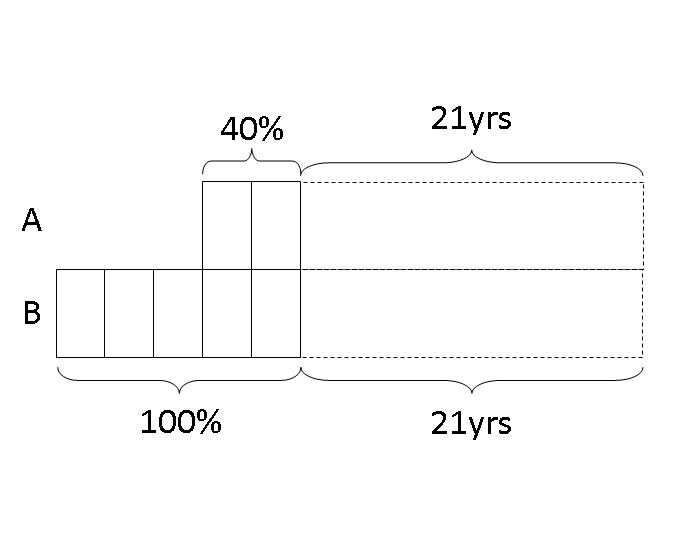
Step 2: Next, we draw an equal bar to the right of both of their models to show they have both grown an equal number of year, i.e., 21 years.
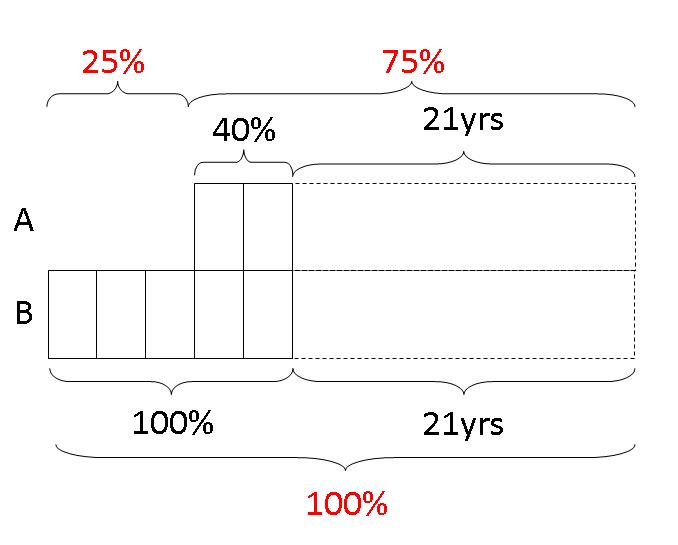
Step 3: After 21 years, A is supposed to be 75% of his brother, so we mark out the total of A's model to be 75% and the total of his brother's model to be 100%. Thus, the difference between their 2 models should be equivalent to 100% - 75% = 25%.
Step 4: From the model, we can see that 25% is equivalent to 3 units. Then, 75% must be equivalent to 3 x 3 units = 9 units. Since A already has 2 units before growing another 21 years, the remaining 21 years must be equivalent to 9 units - 2 units = 7 units. So, we divide the long bar into 7 equal units and do likewise for B's model.
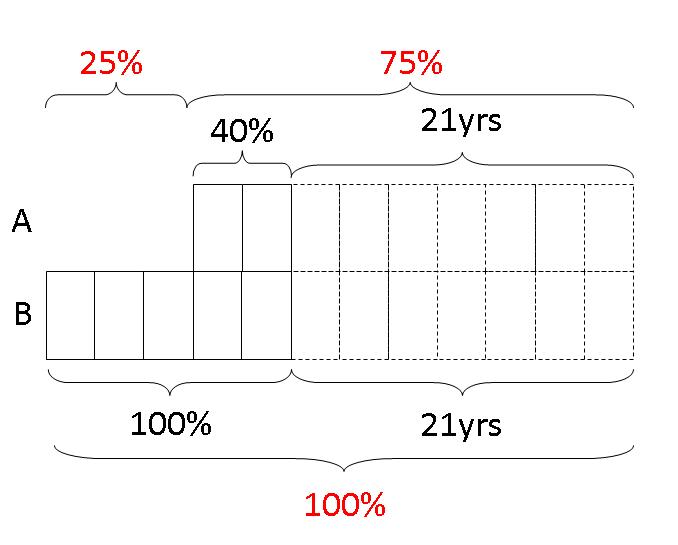
From the model,
7 units ---------- 21 years
1 unit ---------- 21 years / 7 = 3 years
2 units ---------- 2 x 3 years = 6 years
Therefore, A is 6 years old now.
Go To Top - Model Method - Questions and Answers
If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!




