Model Method - Questions and Answers

Question posted by Sandy from the United States:

Grade/Level: 5th Grade

Question: Joe and Moe were on the bus last Monday when a sneaky pickpocket stole some of their money. They went back home and counted their money. Joe had $91 more than Moe so he gave Moe 2/5 of his money. Joe had 6/7 as much money as Moe after that. How much money did Joe have before he gave Moe some?

Answer:


Step 1: This question involves the Constant Total Concept. For this question, it is easier to work backwards as there is a "Multiples Relationship" between the before and after model(i.e. Joe had 6/7 as much money as Moe after that.). We draw 6 boxes to represent the total amount of money Joe had and 7 boxes to represent the amount of money Moe had after the transfer.

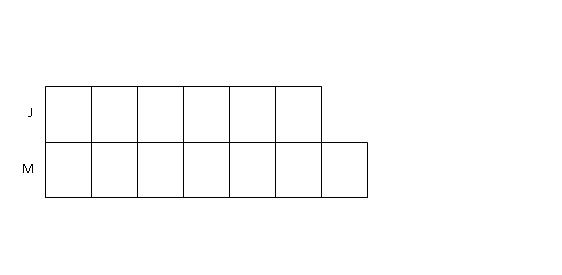
Step 2: If Joe gave 2/5 of his money to Moe, then he must have 3/5 of his money left. So we mark the remaining 6 units of Joe's money as 3/5.

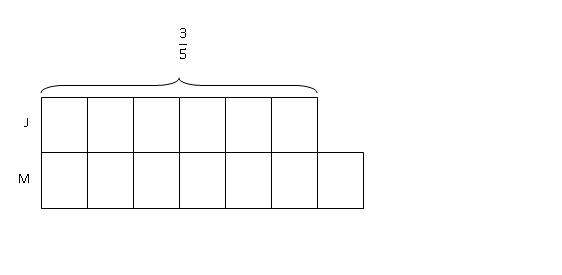
Step 3: Working backwards, we will now "transfer" the 2/5 given to Moe back to Joe. Since 3/5 is equivalent to 6 unit, then 2/5 must be equivalent to 4 units. we draw this 4 units in dotted lines as they do not belong to Joe now.

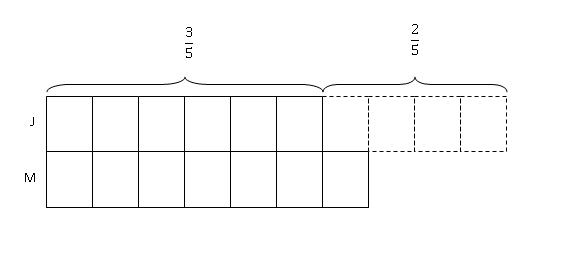
Step 4: We were also told in the question that Joe had $91 more than Moe. Before the transfer, Joe should have 10 units and Moe 3 units. So we mark the difference between their money, i.e. 10 units - 3 units = 7 units as $91.

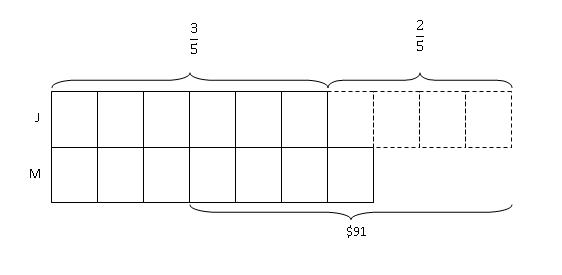
From the model,

7 units ---------- $91

1 unit ---------- $91 / 7 = $13

10 units ---------- 10 x $13 = $130

Therefore, Joe had $130 before he gave Moe some money.

Go To Top - Model Method - Questions and Answers


If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!