Model Method - Questions and Answers
Question posted by Christina from Singapore:
Grade/Level: Primary 5
Question solved by Model Method: Alvin,Brandon and Calvin bought a present for their father. Alvin paid 1/3 of the total amount paid by Brandon and Calvin. Brandon paid 1/5 of the total amount paid by Alvin and Calvin. If Calvin paid $60 more than Brandon, how much did the present cost ?
Answer:
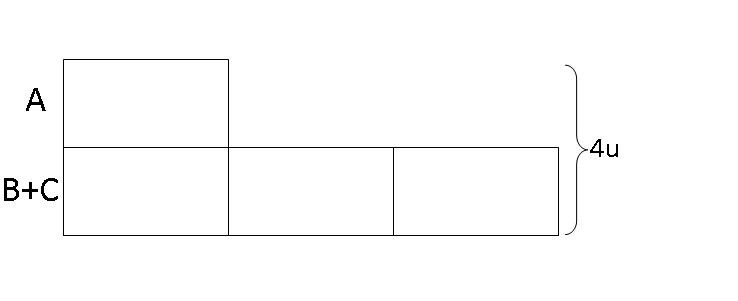
Step 1: Since Alvin paid 1/3 of the total amount paid by Brandon and Calvin, we draw 1 box to represent the amount paid by Alvin and 3 boxes to represent the total amount paid by Brandon and Calvin. We can see that the total of the three of them is 4 boxes.
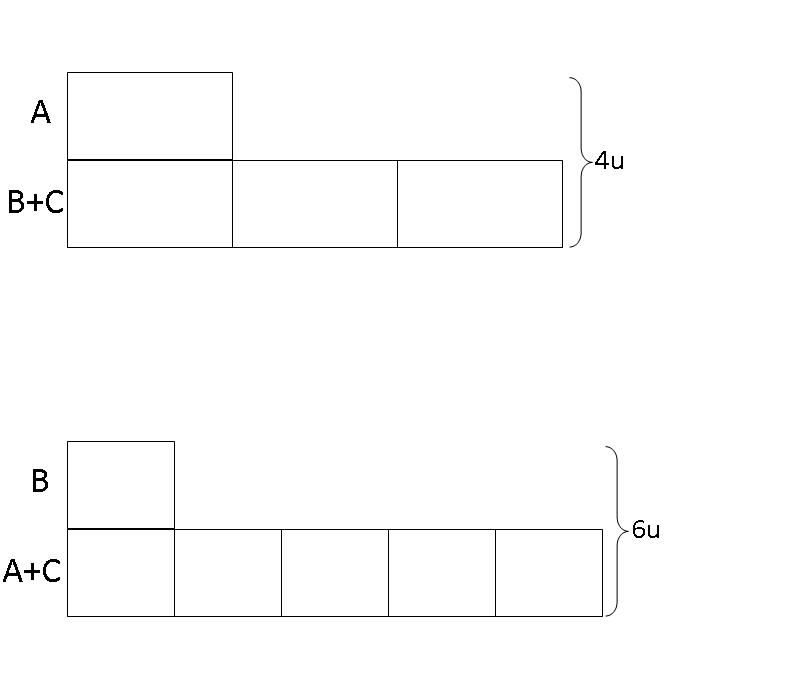
Step 2: Since Brandon paid 1/5 of the total amount paid by Alvin and Calvin, we draw a second model using 1 box to represent the amount paid by Brandon and 5 boxes to represent the total amount paid by Alvin and Calvin. We can see that the total of the three of them is 6 boxes.
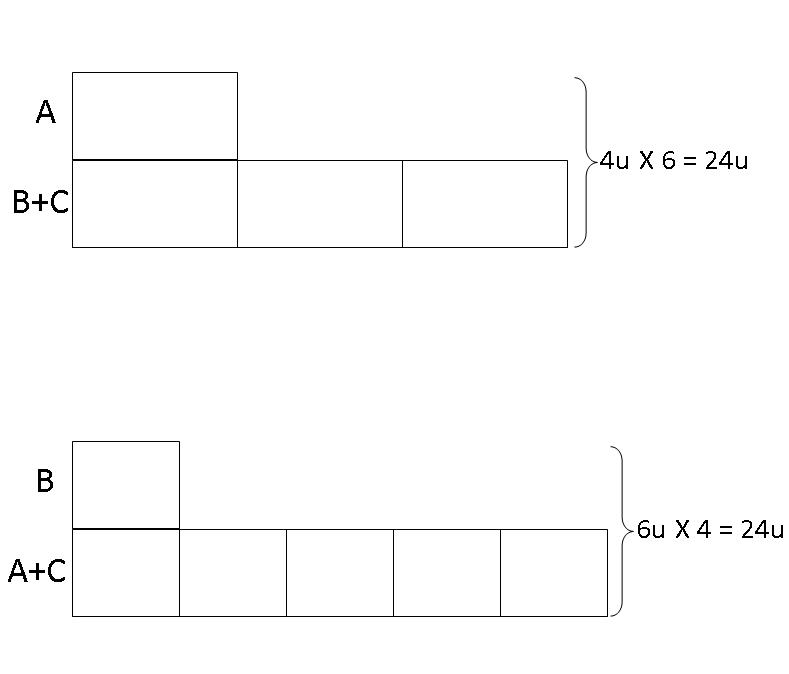
Step 3: As the total of the first model and the total of the second model are equal, i.e. A + (B and C) is equal to B + (A and C), we can make the units in both models become equal sized by finding the common multiple of 4 boxes and 6 boxes, which is 24 units.
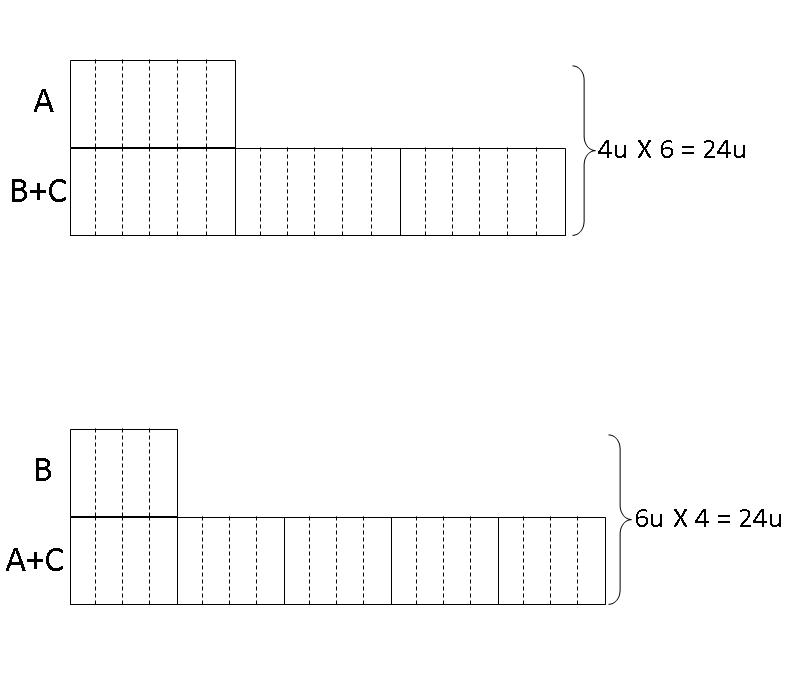
Step 4: For the first model, the total of the 4 boxes represent 24 units, so each box represents 6 units. Thus, we sub-divide each box into 6 units. For the second model, the total of the 6 boxes represent 24 units, so each box represents 4 units. Thus, we sub-divide each box into 4 units.
Step 5: From the first model, we can see that Alvin has 6 units and we use a bracket to denote that. We then apply this newfound information to the second model and mark out 6 units as Alvin's share.
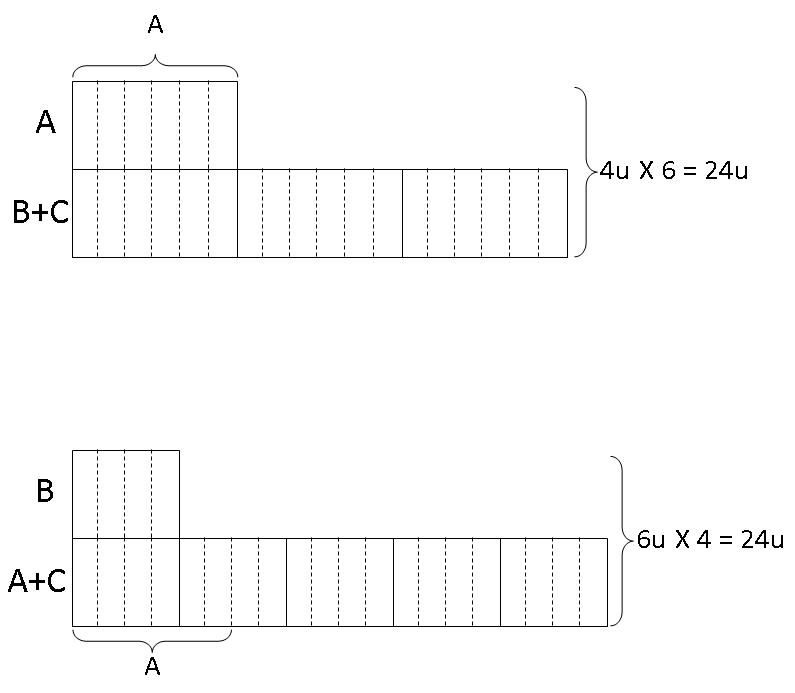
Step 6: From the second model, we can see that Brandon has 4 units and we use a bracket to denote that. We then apply this newfound information to the first model and mark out 4 units as Brandon's share.
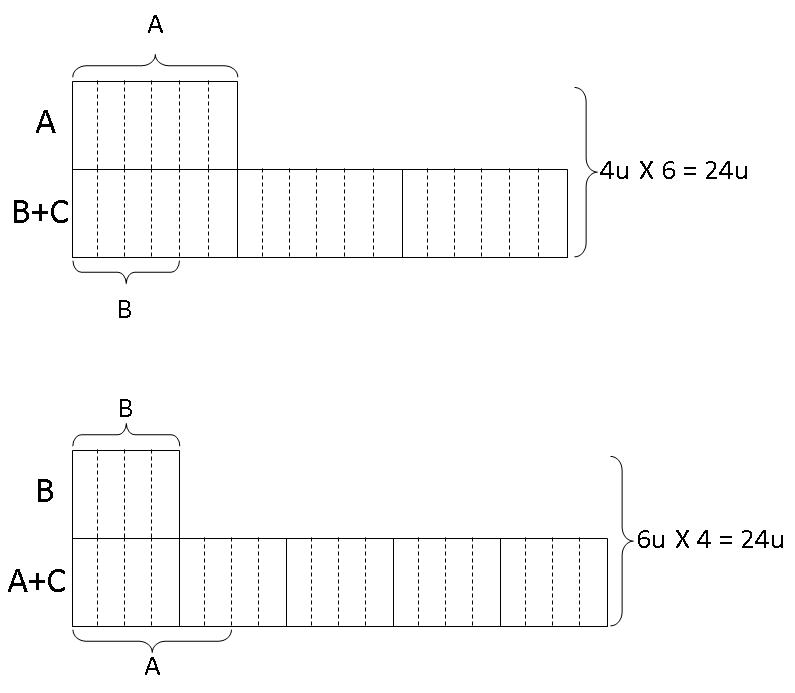
Step 7: From the first model, we can see that the remaining units in the row denoting "B + C" represent Calvin's share. From the second model, we can see that the remaining units in the row denoting "A + C" represent Calvin's share. Take note that both equals to 14 units (both should be equal to same number of units since they both represent Calvin's share).
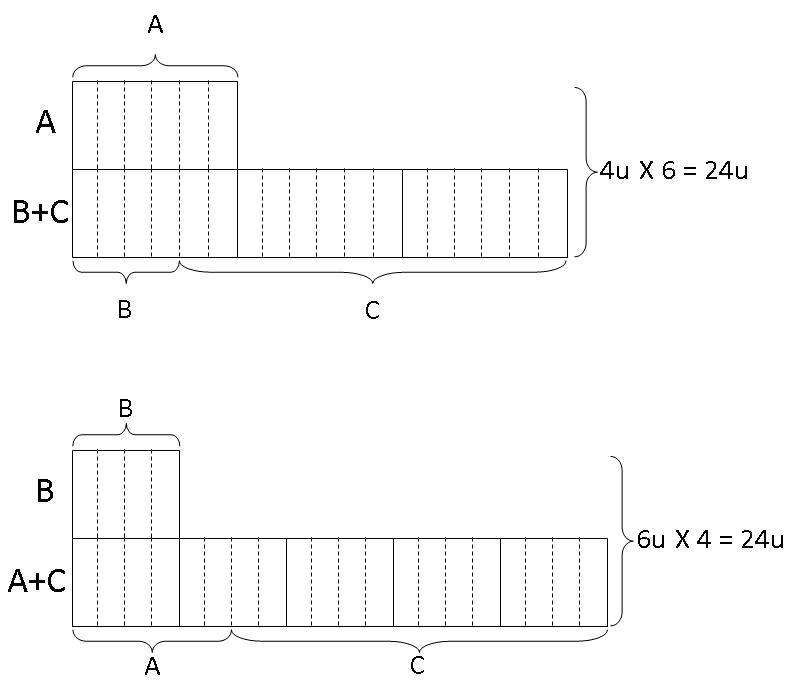
Step 8: Since Calvin's share is 14 units and Brandon's share is 4 units and Calvin paid $60 more than Brandon, then 10 units(14 units - 4 units) must be equal to $60.
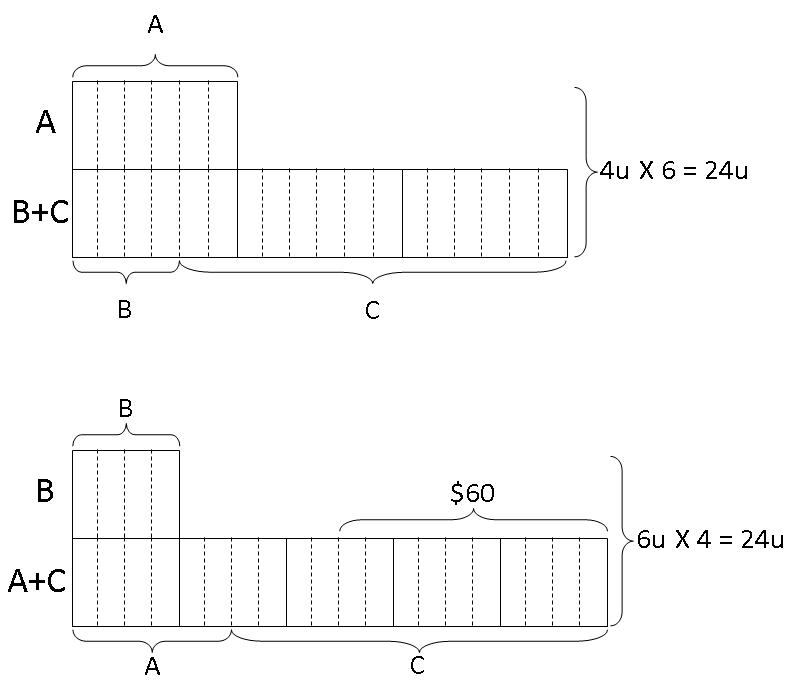
14 units - 4 units = 10 units
10 units ---------- $60
1 unit ---------- $60 / 10 = $6
24 units ---------- $6 X 24 = $144
Therefore, the cost of the present is $144.




