Model Method - Questions and Answers
Question posted by Sharon from Singapore:
Grade/Level: P3
Question solved by Model Method: Ken and Lionel had the same amount of money. After Ken received an additional amount the same as what he had and Lionel spent $7, Ken had thrice as much as Lionel. How much did Lionel have at first?
Answer:
Step 1: First draw 2 identical boxes to represent the amount of money Ken and Lionel had.
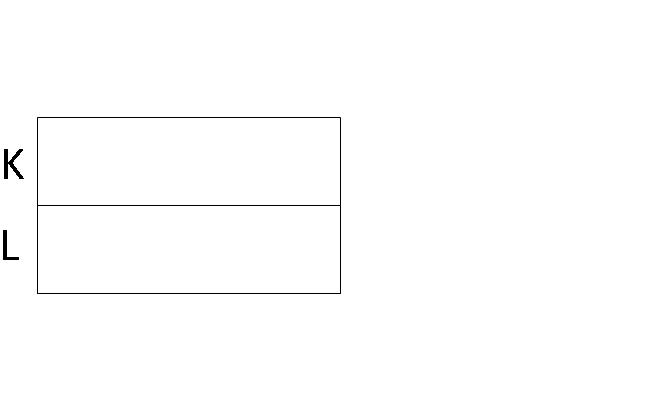
Step 2: Since Ken received an additional amount the same as what he had, we draw 1 identical box to the right of Ken to represent the amount of money he received.
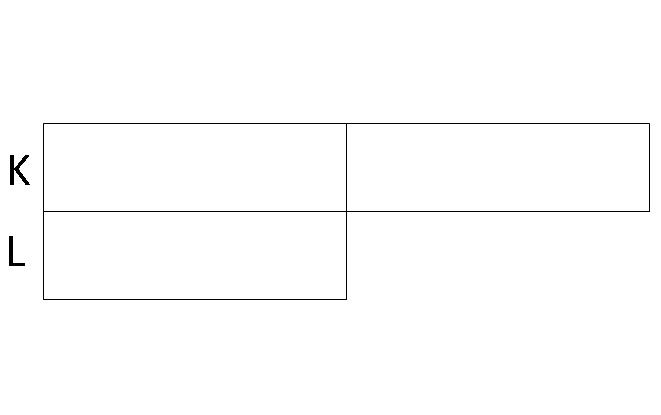
Step 3: Since Lionel spent $7, we mark out a part of his model as $7 spent.
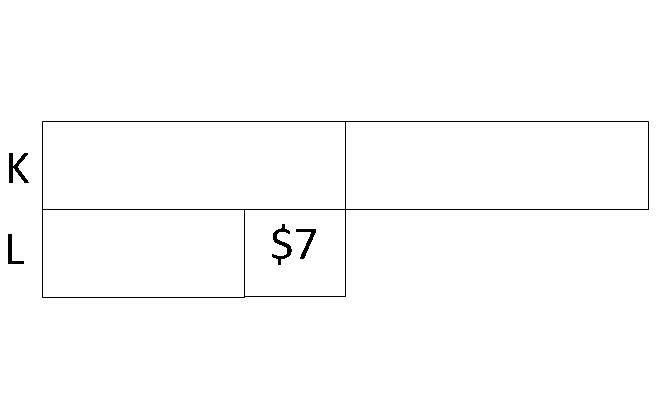
Step 4: We then mark out an equivalent box of $7 from each of Ken's 2 boxes to make all the unknown parts equal. (Note: Models are only useful when all or some of the unknown parts are equal.)
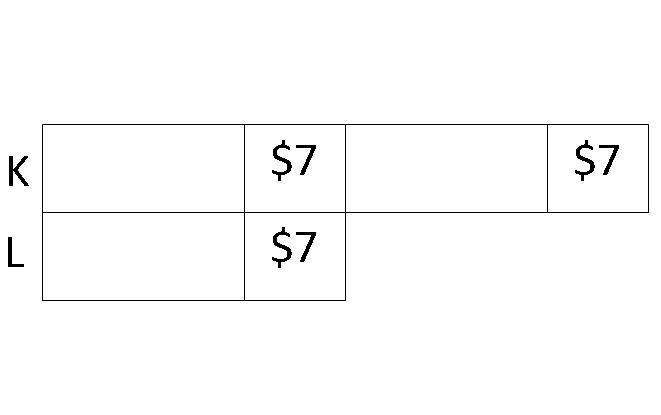
Step 5: Since Ken had thrice as mush as Lionel after all the changes, we mark out the unknown box of Lionel as 1 part. And Ken should have 3 parts.
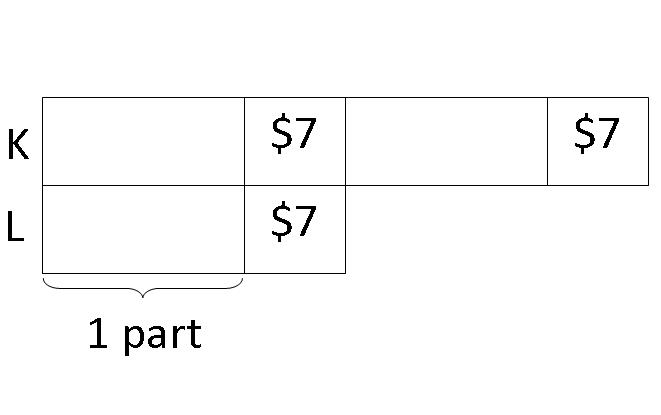
Step 6: Since Ken's 2 unknown parts are identical to Lionel's unknown part, we can label them as 2 parts out of the 3 parts Ken was supposed to have after the changes.
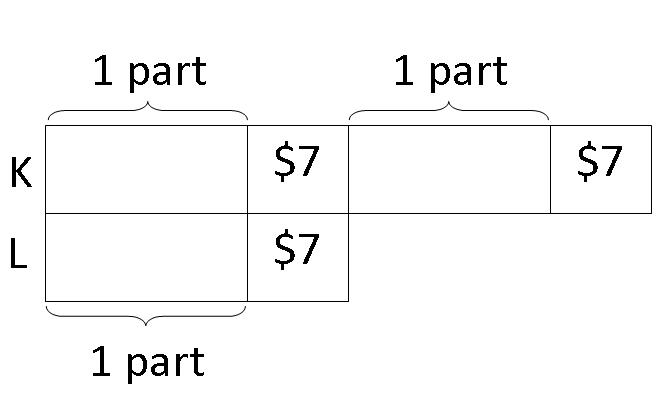
Step 7: Thus, the remaining 2 boxes of $7 should form the last part of Ken's 3 parts after the changes.
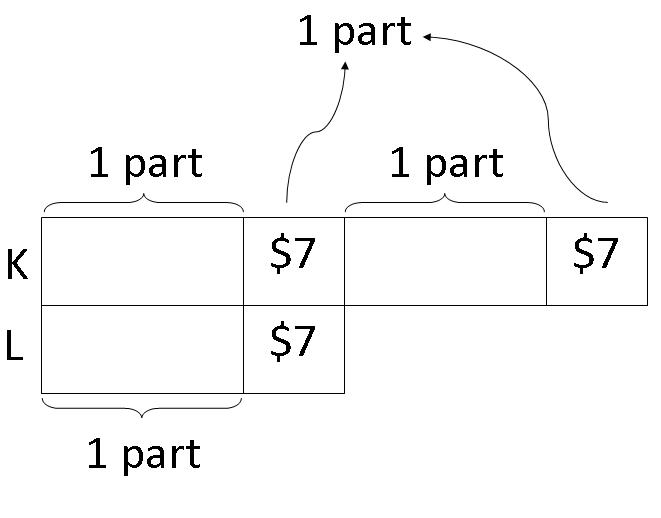
Then, we can say that,
1 part ---------- $7 + $7 = $14
$14 + $7 = $21
Therefore, Lionel had $21 at first.




