Model Method - Questions and Answers
Question posted by Yarn Xee from Singapore:
Grade/Level: Primary 6
Question solved by Model Method : Half the number of people in a boat was female. There were an equal number of children and women in the boat. If there were 100 males and there were 10 more men than children, what percentage of the people were girls?
Answer:
Note: I suspect there was an error in the numbers given in the question as you would see below that we could not get nice whole number for the quantity of people in the question.
Step 1: We can easily solve this question by the model method. Draw 2 equal long bars to represent the number of men and women respectively. Since there were 10 more men than women, we draw another box to the left of men to represent the 10 extra men.
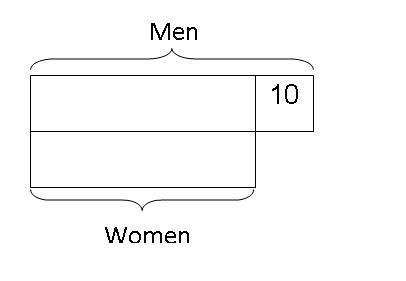
Step 2: Next, draw a box to the left of the men to represent the total number of boys and label it "B" to represent boys.
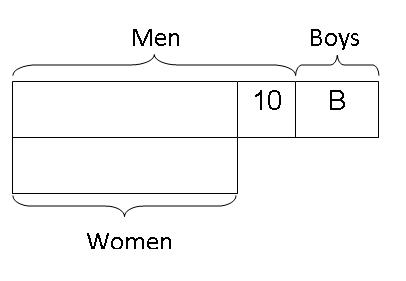
Step 3: Draw another box to the left of women to represent the total number of girls. Since it was given in the question that half of the people in the boat were female, the other half must be males. So, there should be an equal number of males and females. Hence we draw the "girls" box to coincide with the end of the "boys" box thereby making the total of men and boys equal to the total of women and girls.
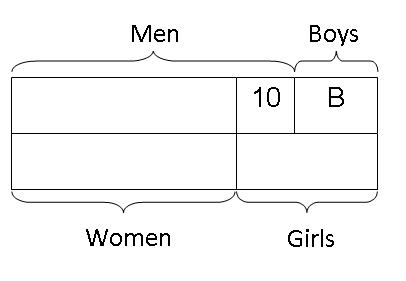
Step 4: Since the length of the girls coincide with the length of the boys plus the box with "10", then the total number of girls must be equal to the total number of boys plus 10.
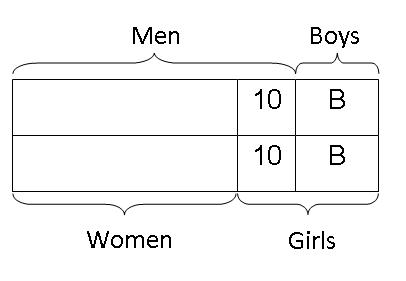
Step 5: As the total number of women is equal to the total of all the boys and girls, the total number of women must be equal to 2 units of "B" and 1 unit of "10".
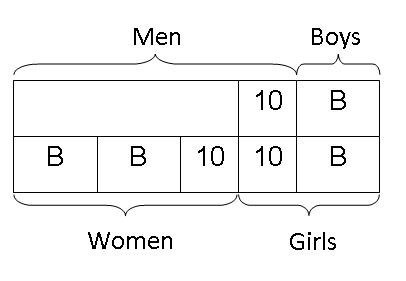
Step 6: As the total number of men is equal to the total number of women plus 10, the unknown part of the men must also be equal to 2 units of "B" and 1 unit of "10". And since it was given in the question that there were 100 males and there were equal number of males and females, we can label the total of males and females to be 100 each.
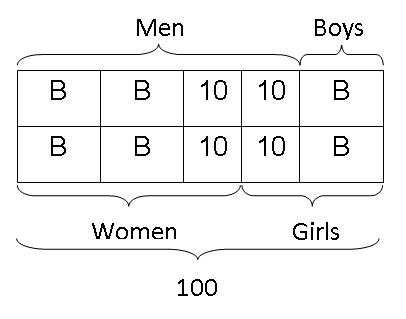
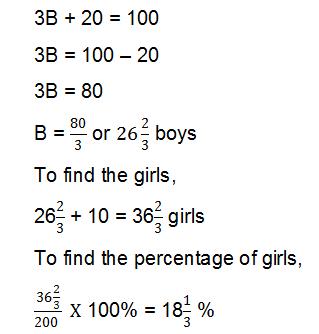
As mentioned earlier, I suspect there is an error in the question. That is why we get 36 2/3 girls and 26 2/3 boys (have to cut up some of the girls and boys ;p). If we were to change the total number of males to 110 (or 140 or 170, etc...), we would be able to get nice whole numbers (no need to cut up anyone :) ).




