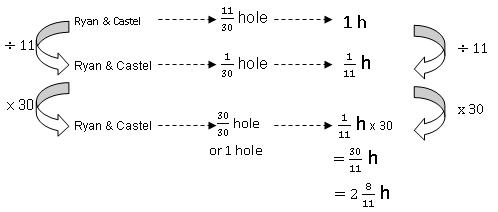Model Method - Questions and Answers

Question posted by Stephanie from country unknown:

Grade/Level: Pre-algebra/Algebra

Question: Working alone, Ryan can dig a 10 ft by 10 ft hole in five hours. Castel can dig the same hole in six hours. How long would it take them if they worked together?

Answer:

It is easier to solve this question using the "3-Lined Method".

In this method, we use the 1st line to depict the relationship given, the 2nd line to reduce the "left side" to 1 unit, and the 3rd line to work out the answer by finding the number of units desired. In some cases, 2 lines are enough when we only want to find the equivalent value for 1 unit.

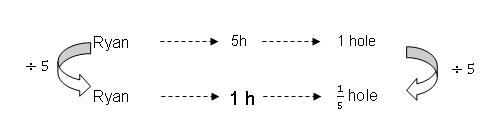
Step 1: Establish the relationship between the 3 variables given, i.e., Ryan can dig a hole in five hours. Take note that we always place the unknown variable that we are trying to work out on the right side. Then reduce the left side variable to 1 unit, in this case, divide by 5. To balance it, we need to do the same to the right, also divide by 5.

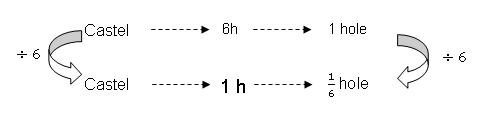
Step 2: Similarly,we also establish the relationship for Castel between the 3 variables given, i.e., Castel can dig the same hole in six hours. Then reduce the left side variable to 1 unit, in this case, divide by 6. To balance it, we need to do the same to the right, also divide by 6.

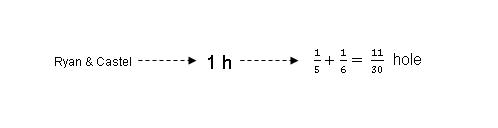
Step 3: Combining Step 1 and Step 2, we get

Step 4: Next, we rearrange the 3 variables so that the unknown (number of hours) is on the extreme right side.

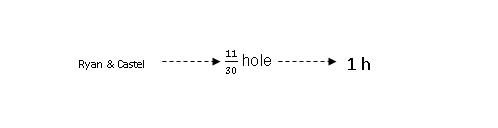
Step 5: Continue to work out values of 1 unit (1/30 hole) and 30 units (30/30 hole or 1 complete hole).