Model Method - Questions and Answers
Question posted by Tracey from the United States:
Grade/Level: 4th Grade
Question solved by Model Method: The average number of red, blue, and green beanbags in a store is 136. There are 30 more red beanbags than blue beanbags. There are 15 fewer green beanbags than blue beanbags. How many green beanbags are in the store?
Answer:
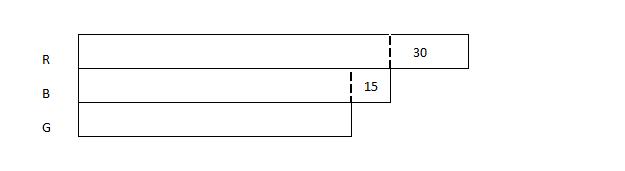
Step 1: This question involves the Comparison Concept. Since there are 30 more red beanbags than blue beanbags, we draw 1 long bar to represent the number of blue beanbags and another bar which is longer by 30 to represent the number of red beanbags.

Step 2: Next, we compare the number of green beanbags with the number of blue beanbags. Since there are 15 fewer green beanbags than blue beanbags, we draw 1 bar shorter than the bar representing the blue beanbags by 15 to represent the number of green beanbags.
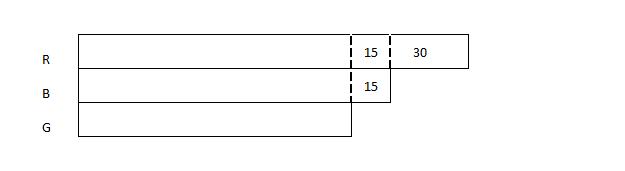
Step 3: Next, we make all the unknown parts equal by cutting the unknown portion of the red beanbags' model to reflect the part that is equal to 15. The remaining unknown part is now equal to the other 2 unknown parts of the models of the green beanbags and blue beanbags.
Step 4: Lastly, we draw a bracket to the right of the models to show the total of all the beanbags. This total can be easily worked out by multiplying the average number of beanbags by 3 types of beanbags to get a total of 408.
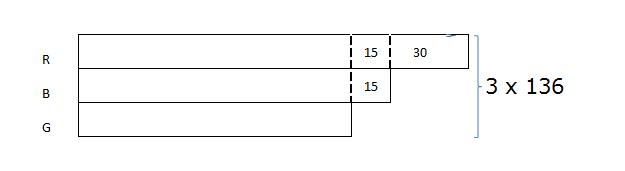
From the model,
3 units ----------> 408 - 15 - 15 - 30 = 348
1 unit ----------> 348 / 3 = 116
Therefore, there are 116 green beanbags.
If you want us to send you our future Modelmatics eZine that would inform you on the latest article in Teach Kids Math By Model Method, do an easy sign-up below. Subscription is FREE!




